Ito's Stochastic Calculus And Probability Theory

As the name suggests stochastic calculus provides a mathematical foundation for the treatment of equations that involve noise. For almost all modern theories at the forefront of probability and related fields Itos analysis is indispensable as an essential.

Ito Stochastic Calculus Springerlink

Kp Itos Stochastic Calculus and Probability Theory av Nobuyuki Ikeda Sinzo Watanabe Masatoshi Fukushima Hiroshi Kunita p.

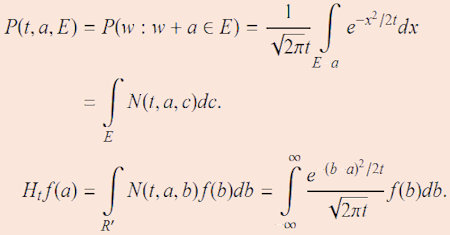
Ito's stochastic calculus and probability theory. May someone please recommend a book or website where one can learn Stochastic Calculus and Ito processes from scratch. 1996 Lvys stochastic area formula and Brownian motion on compact Lie groups. 10112008 A recent monograph entitled Itos Stochastic Calculus and Probability Theory 1996 dedicated to Ito on the occasion of his eightieth birthday contains papers which deal with recent developments of Itos ideas-.

Recall that a stochastic process is a probability distribution over a set of paths. Stochastic Di erential Equations 67 1. Itos Stochastic Calculus and Probability Theory.

Ikeda Nobuyuki Watanabe Sinzo Fukushima Masatoshi Kunita Hiroshi. Stochastic processes - random phenomena evolving in time - are encountered in many disciplines from biology through geology to finance. Probability-theory reference-request stochastic-processes stochastic-calculus.

Although Ito first proposed his theory now known as Itos stochastic analysis or Itos stochastic calculus about fifty years ago its value in both pure and applied mathematics is. Quadratic Variation and Covariation 54 3. Stochastic calculus and the Stratonovich stochastic calculus.

In maths its difficult to say whats a field or a subfield. Professor Kiyosi Ito is well known as the creator of the modern theory of stochastic analysis. This course focuses on mathematics needed to describe stochastic processes evolving continuously in time and introduces the basic tools of stochastic calculus which are a cornerstone of modern probability theory.

Collection of the Formal Rules for Itos Formula and Quadratic Variation 64 Chapter 6. Each of the two. Skickas inom 10-15 vardagar.

It is very clearly explained baby Rudin is all you need. Its Stochastic Calculus and Probability Theory. In the field of probability theory we are interested in probability models having a dy-namic structure ie.

A time evolution governed by endogeneous correlation properties. The aim was to introduce the theory of stochastic integration in as direct and natural way as possible without losing any of the mathematical rigour. There are two dominating versions of stochastic calculus the It.

Watanabe S Ikeda N Fukushima M Kunita Hiroshi Ikeda Nobuyuki Watanabe Sinzo Fukushima Masatoshi. For which we are highly motivated. Such probability models are called stochastic processes.

Id just say they are different fields with different connections. In the analysis of phenomena with stochastic dynamics Itos stochastic calculus 15 16 8 23 19 28 29 has proven to be a powerful and useful tool. A change of measure of a stochastic process is a method of shifting the probability distribution into another probability distribution.

Eds Its Stochastic Calculus and Probability Theory. De nitions 67 2. Ikeda N Watanabe S Fukushima M Kunita H.

Itos Formula for Brownian motion 51 2. Full Multidimensional Version of Ito Formula 60 5. It has a lot of easy exercises that build confidence that you understand basic concepts.

Brownian motion or the Wiener process was discovered to be exceptionally complex mathematically. I decided to use this blog to post some notes on stochastic calculus which I started writing some years ago while learning the subject myself. 2952007 This course is about stochastic calculus and some of its applications.

Half of these have solutions. Active 6 years 11 months ago. The required background for properly understanding these notes is measure theoretic probability theory.

Publisher Name Springer Tokyo. Professor Kiyosi Ito is well known as the creator of the modern theory of stochastic analysis. These will be probability theory and stochastic calculus.

Probability theory has connections with measure theory and that measure is given by Lebesgue integrals for continuous. In this section we x a nal time Tand suppose that. Thus it requires its own rules of calculus.

The various problems which we will be dealing with both mathematical and practical are perhaps best illustrated by consideringsome sim-. Stochastic Calculus 51 1. It develops all the measure theory you need in a probability context.

A central ingredient of this calculus is the Ito formula 15 16 23 a change of variable formula for functions fX t of a semimartingale Xwhich. The Wiener process is almost surely nowhere differentiable. Although Ito first proposed his theory now known as Itos stochastic analysis or Itos stochastic calculus about fifty years ago its value in both pure and applied mathematics is becoming greater and greater.

Stochastic Calculus Notes. The last chapter whets your appetite for stochastic calculus and he gives suggested reading. Itos Formula for an Ito Process 58 4.

Elementary Stochastic Calculus With Finance In View Advanced Series On Statistical Science And Applied Probability Book 6 Thomas Mikosch Amazon Com Books

Stochastic Calculus And Model Of The Behavior Of

Stochastic Calculus A Practical Introduction Probability And Stochastics Series Book 6 1 Durrett Richard Amazon Com

Probability And Stochastic Processes Wiley

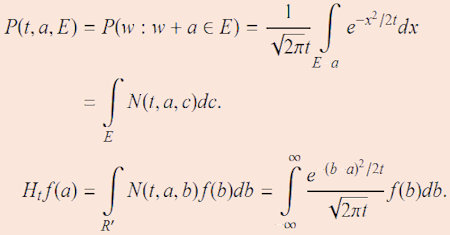
Stochastic Calculus Free Books At Ebd